Navigation Basics

Navigation Basics: Fundamental Concepts in Aeronautical Navigation

In order to describe the navigation basics let us first define a few terms and explain some fundamentals.

The Earth

Geographic Poles

For navigational purposes the shape of the earth is approximated by an ideal sphere. The axis on which the earth rotates is called the geographic Polar Axis. The two points where the axis meets the surface of the sphere are called:

* the North Geographic Pole - or True North; and

* the South Geographic Pole - or True South. If the earth was cut through the centre in the plane in which it rotates, then the hemisphere that accomodates the North Pole (which, in common terms, equates to the surface of the "top half" of the sphere) is referred to as the Northern Hemisphere. Consequently the "bottom half" would be the Southern Hemisphere. The circle that forms along this cutting plane and the surface of the sphere is called the equator. In real terms the diameter of the earth along its axis is smaller than along its rotational plane. The difference is only about 1/300 of the diameter.

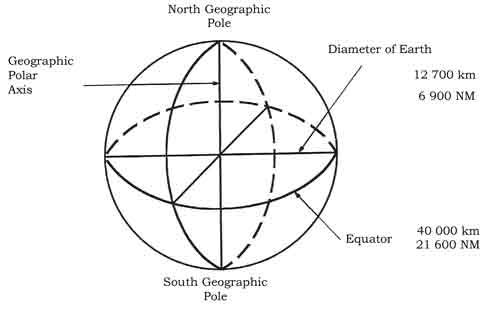
Figure: Terms and dimensions of the Earth. The earth rotates once around from West to East in 24 hours. Looking down onto the North Pole, this rotation is therefore anti-clockwise. The circle that forms at the earth's surface in any plane that passes through the centre of the earth is called a Great Circle (GC). The following things are true for Great Circles:

* A Great Circle is the largest circle that can be drawn on any sphere.

* The shortest distance between any two points on the surface of a sphere is the arc of a Great Circle.

* An infinite number of Great Circles can be drawn on a sphere through two points that are diametrically opposed. On earth the geographic poles are two such points that take special significance in this respect. The resulting Great Circles are called Meridians of Longitude.

* In contrast to the statement above only one Great Circle can be drawn between two points on the surface of a sphere that are not diametrically opposed. The Great Circle that forms in the rotational plane, i.e. in the plane perpendicular to the axis on which the earth rotates and through its centre is called the Equator. A Small Circle is any circle on the surface of a sphere that is not a Great Circle, i.e. the centre of Small Circles is not at the centre of the earth. Parallels of Latitude (other than the Equator are Small Circles.) It is more convenient for a pilot, when using a Magnetic Compass or Direction Indicator, if it is possible for him to fly a constant Track direction. This can be achieved by following a Rhumb Line track, rather than a Great Circle track. A Rhumb Line crosses all meridians of longitude at this same angle and will appear on the surface of the Earth as a curved line concave to the nearer pole. Despite the fact that it might look the shortest on a chart in some projections, a Rhumb Line track is not the shortest track from one point to the other on a sphere. (see further down in the section on projections for an illustration)

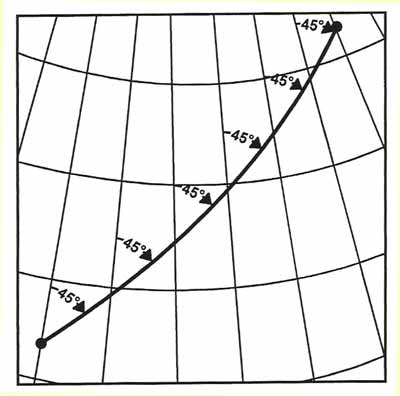
Figure: Rhumb line crosses meridians As mentioned earlier, the shortes track between two points is on the arc of a Great Circle. However, following such a track is rather inconvenient as the direction changes all the time. In practical terms, over long distances, a Great Circle track is approximated by a number of rumb line track segments.

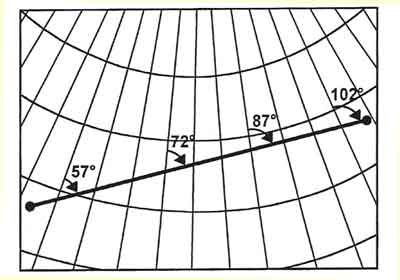
Figure: Great Circle crosses meridians Meridians of Longitude

There are an infinite number of Great Circles passing through the poles and perpendicular to the equator. In order to reference longitude on the surface of the earth, 180 Great Circles are defined by advancing from one to the next by one degree (measured at the centre of the earth), starting from a basic reference. The basic reference for longitude has been defined as the Greenwich Meridian, also known as the Prime Meridian. It is the half of the Great Circle which passes through the Greenwich Observatory situated near London, as well as the North and South Geographic Poles. The Prime Meridian is designated as 'Longitude 00°'. The other half of the same Great Circle, that contains the Prime Meridian, passes down the Western side of the Pacific Ocean and is known as 'Longitude 180°'. It is also referred to as the Anti-Meridian of Greenwich. Meridians of Longitude are specified by their angular difference in degrees East or West from the Prime Meridian. Each degree of longitude is subdivided in 60 minutes of longitude and each minute in 60 seconds of longitude.

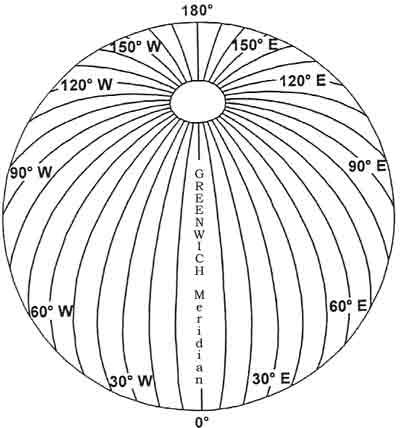
Figure: Meridians of Longitude Parallels of Latitude

The reference for latitude is the Equator (Latitude 00°). Consequently the latitude of a place is its angular distance in degrees from the equator, (measured at the centre of the Earth) and designated either North or South. It follows, that the geographic poles have 90 degrees latitude - either North or South. Circles on the surface that connect points of equal latitude are called Parallels of Latitude. The equator is the longest parallel of latitude and a Great Circle. All the other parallels of latitude are Small Circles and parallel to the equator and to each other. Each degree of latitude is subdivided in 60 minutes of latitude and each minute in 60 seconds of latitude.

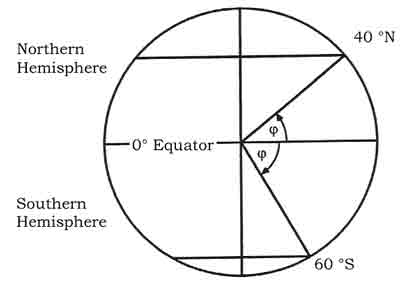
Figure: Latitude

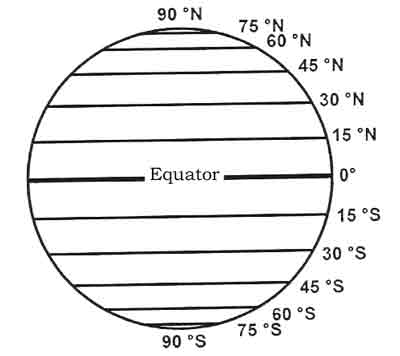
Figure: Parallels Determining position in any coordinate system is based on measurement of direction and distance. Direction and Distance and their expression in projections of the sphere onto a flat surface (called charts) are therefore the most fundamental concepts used in navigation of which the pilot should have a thorough understanding. Another important concept that is connected to these is the expression of time. Direction True Direction

If direction is expressed in reference to the geographic pole, then it is said to be True Direction, and is symbolised by 'T'. True North is therefore written as 000°T (360°T) or 000T (360T). The true direction is what can be determined directly from most charts commonly used in aviation. Sadly, most of the instruments available to the pilot cannot determine the direction of True North. It is therefore necessary to learn about another important system to reference direction, one that can be measured by a compass - the Magnetic North. Magnetic Direction

The surface of the Earth is covered by a weak magnetic field. The lines of the magnetic field exit the earth surface near Hudson Bay in Canada and enter again at a point near South Victoria Land in Antarctica. In between these points, the lines of the magnetic field form a loop of which one half extends above the surface and the other half (the returning bit) beneath the surface of the earth. The entry and exit points of the field through the earth's surface (which is where the field lines are perpendicular to the surface) are called the Magnetic Poles. Because of their proximity to the North and South Geographic Poles, the magnetic poles are referred to as the North Magnetic Pole and the South Magnetic Pole. It is a useful property of a magnetic compass that it aligns to the magnetic field lines and therefore points in the direction of Magnetic North. Unfortunately for navigation, the magnetic poles and the geographic poles are not in the same location and consequently there is a small but significant difference between the True (i.e. geographic) Direction as shown in the chart and the Magnetic Direction as indicated by the compass. Variation

The angular difference from True North to Magnetic North for any point on the earth surface is called Variation and differs from location to location. If the magnetic compass points East of True North then the Variation is said to be East. If the compass points to the West of True North, then the variation is West. Lines that can be drawn between points of equal variation are called Isogonals (or Isogonic Lines). On the ICAO 1:500000 Aeronautical Chart, the Isogonals are shown as dashed lines coloured magenta. If you are on an isogonic line the compass reading can be related to True North. Your compass points to Magnetic North, which will be off the True North by the variation.

Figure: Chart - Magnetic Variation If Magnetic North is to the West of True North (i.e. West Variation), then °M will exceed °T. Conversely, if Magnetic North is to the East of True North (i.e. East Variation), then °M will be less than °T.

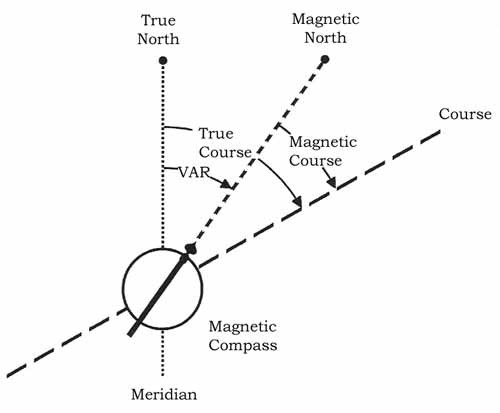
Figure: Variation East

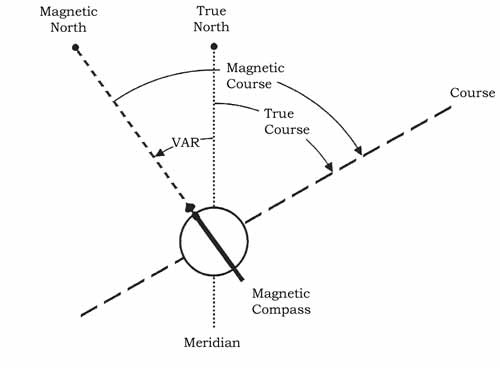
Figure: Variation West An easy way to remember the relationship between True and Magnetic is: VARIATION WEST, MAGNETIC BEST, VARIATION EAST, MAGNETIC LEAST Lines of zero variation (were True North and Magnetic North are in the same direction) are called Agone or Agonic Line. Factors affecting accuracy of compass reading

The Earth's magnetic field is fairly weak, and varies in strength and direction over the entire surface of the Earth. The strength of the magnetic field can be resolved into two components:

* a horizontal component parallel to the surface of the Earth, which is used to align the Compass needle with Magnetic North; and

* a vertical component, which causes the magnetic needle to dip down. The relative proportion of the horizontal and the vertical component changes, depending on the distance from the magnetic pole and equator. The vertical component causing dip gets stonger the closer to the magnetic poles, whereas the horizontal component is most dominant at the equator. As a result the compass is not very accurate as an indicator of Magnetic North at higher latitudes (near the magnetic poles) and on the other hand very stable and accurate in the areas near the equator. At latitudes higher than 60° North or South (i.e. closer to the Poles than 60°N or S), the Magnetic Compass is not very reliable at all. The vertical component of the magnetic field that causes the dip has an important effect on the compass reading when changing orientation of the airplane or when accelerating or decelarating during flight maneouvres. The pilot should be familiar with the effect this has on the accuracy of the compass reading. Acceleration/Deceleration Errors are false compass indications of a swing to the North or South during speed changes of the airplane. This error is most pronounced when flying on a heading of East or West and decreases when flying closer to a North or South heading. In a direct North or South heading this error does not occur. In the Northern Hemisphere, the compass swings towards the North during acceleration and towards the South during deceleration. In the Southern Hemisphere this error occurs the other way round. When the speed stabilises, the error disappears. In contrast, Turning Errors are false compass indications when the airplane is changing direction. Here the error has its most pronounced effect on a North or South heading and the effect disappears when on a East or West heading. As the airplane turns the effect is one of a leading or lagging in compass indication. In the Northern Hemisphere, making a turn from a northerly heading, the compass will indicate first a turn in the opposite direction and then follow the real change of direction, i.e. lag behind. This effect will decrease the more the heading approaches East or West. Turning from West or East towards North the effect will be one of an increasing lag behind the real direction the further the turn progresses towards North. Making a turn to or from a southerly heading, the effect will be a leading effect. The amount of lead or lag is approximately equal to the latitude of the airplane. For instance turning from a heading of South to West while flying at latitude 50°N, the compass will turn to a heading of 230° (180°+50°). Halfway through the turn the heading will be 250° (225°+25°). At the end of the turn the heading will be indicated correctly: 270°. Finally, it is important to recognise that the compass reading is influenced by deformation of the magnetic field around the compass. Common causes are metal items near the compass or electromagnetic fields. This kind of deformation is quite common in airplanes. There are a number of techniques to correct for these. Usually there are residual misreadings which are referred to as Deviation. More details on this can be found in the section on aeronautic instruments. Distance For most navigational purposes pilots use the nautical mile to express distance. The nautical mile is related to the angular measurement of latitude on earth: 1' of latitude = 1 nm, and 1° of latitude = 60 nm However, the metric unit of distance is the metre, with longer distances being measured in kilometres (One Thousand Metres). The kilometre is much shorter than the nautical mile. It is the standard unit for distance in most of Europe and many other parts of the world. In a number of countries (including the US and the UK) distances are measured in statute miles, which is also shorter than a nautical mile but longer than a kilometre. Nautical Miles will not be replaced with a Metric System because of their relationship to the angular measurement of Latitude on the Earth. Mapping Projections

A spherical surface cannot be cut and laid out flat in the way a cylinder or a cone can. Consequently, distortion always occurs when projecting points on the surface of the earth onto a flat chart. A number of projection methods exist to reduce the distortion in aeronautical charts, such as projecting onto either a conical or cylindrical surface (which can then be flattened out to form a sheet). In the Lambert's Conformal Conic projection the chart sheet is formed from a secant cone that cuts the sphere representing the reduced earth at two Standard Parallels of Latitude. Just which two parallels of latitude are chosen by the map-maker depends upon which part of the earth, and how much of it, he wants to represent on that particular chart. The standard parallels are usually mentioned at the bottom or on the side of the chart. There is no distortion along the standard parallels and relatively little distortion North or South of them when only short distances are involved. In this type of projection the Great Circle track appears as a straight line, whereas the rhumb line appears bent away from the pole. In terms of practical navigation, a straight line on the chart does indeed represent the shortest connection between two points. However the appearance that the course is straight is an illusion due to the projection. Therefore, in order to measure the course on the conic projection chart, the distance should be divided into a number of subtracks and the true course measured in the middle of each subtrack.

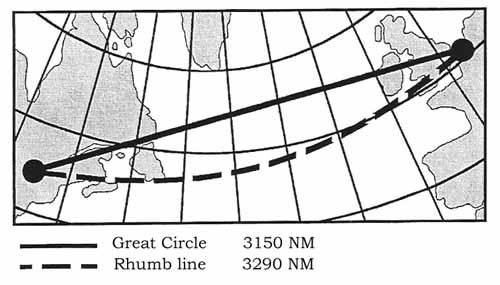
Figure: Rhumb line and Great Circle in conic projection. Another method used frequently is the Mercator projection which is based on projecting points from the surface of the sphere onto a cylinder wrapped around the sphere that touches it at a great circle. An example would be the projection onto a cylinder wrapped around the equator with its sides parallel to the polar axis. A variation of this method is the Transverse Mercator projection which starts with a cylinder wrapped around a chosen meridian of longitude and its anti-meridian, with the sides of the cylinder at 90° to the polar axis. When flattened out, this projection provides a chart with no distortion down the chosen meridian and very little distortion anywhere East or West of this meridian within relatively short distance. In the Mercator projection the rhumb line appears a straight line and the Great Circle track appears bent towards the pole.

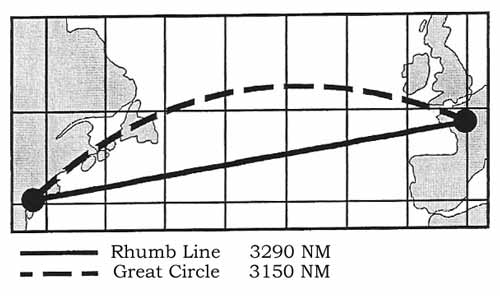
Figure: Rhumb line and Great Circle in Mercator projection Aeronautical charts

Pilotage, which is navigation by reference to landmarks or checkpoints, requires an aeronautical chart showing the surface features of the area in detail which allows pilots to track their position. The aeronautical chart does not only show the topographic and cultural detail but also provides a lot of information on airports, navigational aids and airspace. There are various aeronautical charts available to the VFR Pilot:

* Sectional charts such as the ICAO Aeronautical Charts, scale 1:500 000 (half-million);

* VFR Terminal Area Charts or Topographical Air Charts (in the United Kingdom), scale 1:250 000 (quarter-million);

* World Aeronautical Charts such as the Operational Navigation Chart series (ONC), scale 1:1 000 000 (one million). The ICAO and ONC series charts are based on the Lambert's Conformal Conic projection. The Topographical Air Chart is based on Transverse Mercator projection.

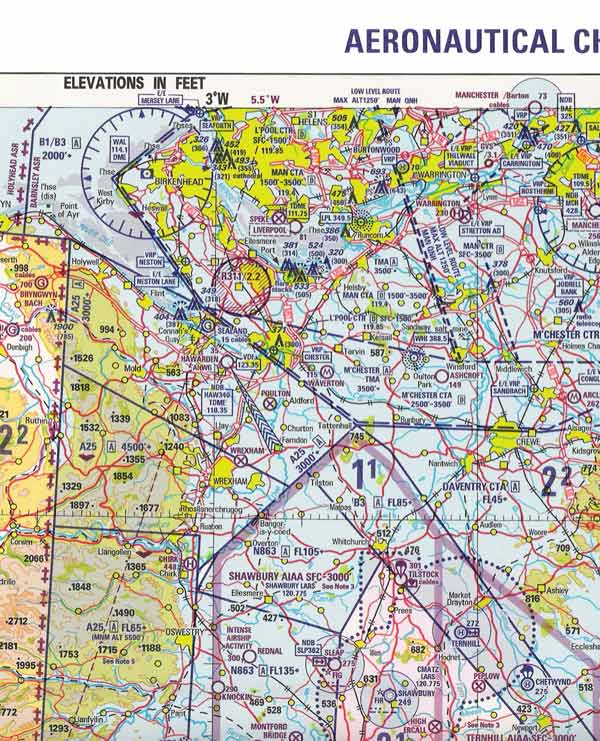
Figure: Example ICAO Aeronautical Chart Important properties of aeronautical charts are Conformity and Equivalence. Conformity

Conformity describes the property of aeronautical charts such as the 1:500,000 and 1:250,000 that they preserve angular relationships i.e. angles and bearings are very accurate. Scale

Scale is defined as the ratio of the Chart Length compared to the Earth Distance that it represents, both measured in the same unit. The larger the scale, (i.e. the greater the chart length for a given distance on earth) the more detail that can be shown. Scale Can Be Expressed in Various Ways:

* as a Representative Fraction. For instance, the WAC and the ONC series are 1:1,000,000 charts (one to a million), where 1 centimetre on the chart will represent 1,000,000cm or 10 kilometres on the earth, or where 1 nm on earth is represented by 1 millionth of a nautical mile on the chart.

* as a Graduated Scale Line, which is usually situated at the bottom of the chart. A graduated scale line allows you to measure-off the distance between two points on the chart and match it against the scale line. Make sure that you use the correct scale line (usually nautical miles), since there may be various ones so that nautical miles, statute miles or kilometres can be measured.

* in Words - e.g. '1 cm equals 5 nm', which obviously means that 5 nm on the earth's surface is represented by 1 cm on the chart.

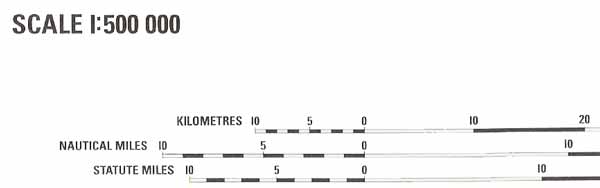
Figure: Chart - Scale Even if there is no scale line on the chart, one can always compare the distance between two places on the chart with the latitude scale which runs down the side of the chart, remembering that 1' of latitude = 1 nm, and 1° of latitude = 60 nm. (NB. 1 degree (1°) is equal to 60 minutes (60')) Equivalence

Equivalence refers to a constant scale over the entire chart in practical terms, i.e. distances can be measured directly from the chart. On conic projections (ICAO 1:500 000), use the latitude scale about midway between the two places, because on some charts scale may vary slightly depending upon proximity to the Standard Parallels. In practical terms, however, scale can be considered as constant over all of a 1:500 000 chart. On Transverse Mercator 1:250 000 charts, the scale is exactly correct at the reference meridian for the chart (2°W for the UK Topographical Air Chart), and can be considered as constant to about 300 nm either side of this. Therefore, to all intents and purposes, scale may be considered constant at all points on both aeronautical chart series, quarter- and half-million. Depiction of height

There are a number of ways of depicting relief. Contours - lines joining places of equal elevation above mean sea level - are common to most charts. The spacing between contour lines is a measure for the steepness of the terrain and differs from chart to chart. Colour or tints are used for various ground elevations. Check the relief portrayal section on the chart for the details.

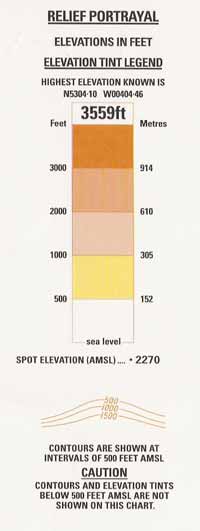
Figure: Chart - Relief Portrayal Spot Elevations (or Spot Heights) are another common indication of elevation and are displayed using a black spot with an adjacent number to indicate the elevation (height AMSL - Above Mean Sea Level) in feet. Spot Elevations show local peaks and other critical elevations that are significantly higher than the surrounding terrain. The highest point on the chart has its elevation printed slightly larger than the rest and is printed in a white rectangle with a black edge. It is also shown on the Relief Portrayal table. A third way of indicating elevation is the Maximum Elevation Figures (MEF).

Figure: Chart - Maximum Elevation Figures Time Universal Coordinated Time (UTC) and Local Mean Time (LMT)

UTC (formerly GMT) is the internationally recognised standard time to which the Local Mean Time (LMT) is referenced. UTC is the time at the Greenwich meridian (0° of longitude) and is often referred to as Zulu time. Meridians to the East are ahead of UTC (one hour per 15° of longitude), and those to the West are behind. These sections between meridians 15° of longitude apart roughly define the Time Zones, where LMT changes by one hours for each time zone. Time zones should be taken into account when planning long flights East or West in particular when determining landing time before sunset is concerned. This can be remembered as: "Longitude East, Universal Least" & "Longitude West, Universal Best" For daylight saving time one hour should be subtracted from LMT.

Definition of sunrise and sunset times

Sunrise occurs when the first part of the sun is just visible on the horizon (when viewed from the ground). Sunset occurs when the uppermost part of the sun is just disappearing below the horizon (when viewed from the ground). A PPL rated pilot (without a Night, IMC or Instrument Rating) is only permitted to fly 30 minutes before sunrise until no later than 30 minutes after sunset. This concludes the Navigation Basics Page.