Weight and balance - meaning and basic calculations
Compliance with the weight and balance limits of any airplane is critical to flight safety. Operating an airplane above the maximum weight limitation compromises the structural integrity of the airplane and adversely affects its performance. Operation with the center of gravity (CG) outside the approved limits may result in control difficulty.
Weight control
Weight is the force with which gravity attracts a body toward the center of the earth. It is a product of the mass of a body and the acceleration acting on the body.
Weight is a major factor in airplane construction and operation, and demands respect from all pilots.
The force of gravity continually attempts to pull the airplane down toward earth. The force of lift is the only force that counteracts weight and sustains the airplane in flight. However, the amount of lift produced by an airfoil is limited by the airfoil design, angle of attack, airspeed, and air density. Therefore, to assure that the lift generated is sufficient to counteract weight, loading the airplane beyond the manufacturer’s recommended weight must be avoided. If the weight is greater than the lift generated, the airplane may be incapable of flight.
Effects of weight
Any item aboard the airplane that increases the total weight is undesirable as far as performance is concerned. Manufacturers attempt to make the airplane as light as possible without sacrificing strength or safety.
The pilot of an airplane should always be aware of the consequences of overloading. An overloaded airplane may not be able to leave the ground, or if it does become airborne, it may exhibit unexpected and unusually poor flight characteristics. If an airplane is not properly loaded, the initial indication of poor performance usually takes place during takeoff.
Excessive weight reduces the flight performance of an airplane in almost every respect. The most important performance deficiencies of the overloaded airplane are:
• Higher takeoff speed.
• Longer takeoff run.
• Reduced rate and angle of climb.
• Lower maximum altitude.
• Shorter range.
• Reduced cruising speed.
• Reduced maneuverability.
• Higher stalling speed.
• Higher approach and landing speed.
• Longer landing roll.
• Excessive weight on the nosewheel or tailwheel.
The pilot must be knowledgeable in the effect of weight on the performance of the particular airplane being flown. Preflight planning should include a check of performance charts to determine if the airplane’s weight may contribute to hazardous flight operations.
Excessive weight in itself reduces the safety margins available to the pilot, and becomes even more hazardous when other performance-reducing factors are combined with overweight. The pilot must also consider the consequences of an overweight airplane if an emergency condition arises. If an engine fails on takeoff or airframe ice forms at low altitude, it is usually too late to reduce the airplane’s weight to keep it in the air.
Weight changes
The weight of the airplane can be changed by altering the fuel load. Gasoline has considerable weight—6 pounds per gallon—30 gallons may weigh more than one passenger. But it must be remembered that if weight is lowered by reducing fuel, the range of the airplane is decreased. During flight, fuel burn is normally the only weight change that takes place. As fuel is used, the airplane becomes lighter and performance is improved.
Changes of fixed equipment have a major effect upon the weight of the airplane. An airplane can be overloaded by the installation of extra radios or instruments.
Repairs or modifications may also affect the weight of the airplane.
Balance, stability, and center of gravity
Balance refers to the location of the center of gravity (CG) of an airplane, and is important to airplane stability and safety in flight. The center of gravity is a point at which an airplane would balance if it were suspended at that point.
The prime concern of airplane balancing is the fore and aft location of the CG along the longitudinal axis.
The center of gravity is not necessarily a fixed point; its location depends on the distribution of weight in the airplane. As variable load items are shifted or expended, there is a resultant shift in CG location. The pilot should realize that if the CG of an airplane is displaced too far forward on the longitudinal axis, a nose-heavy condition will result. Conversely, if the CG is displaced too far aft on the longitudinal axis, a tail-heavy condition will result. It is possible that an unfavorable location of the CG could produce such an unstable condition that the pilot could not control the airplane.
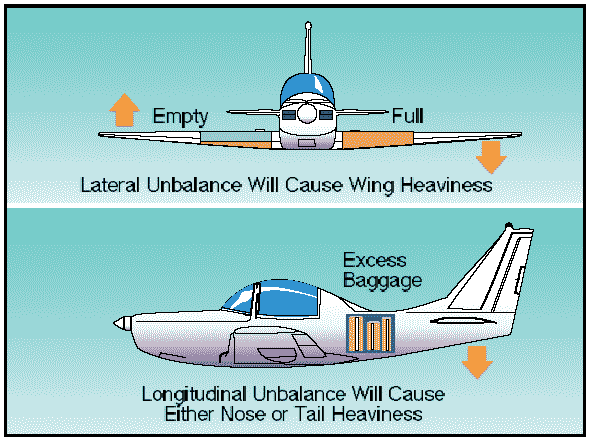
Figure 1: Lateral or longitudinal unbalance.
Location of the CG with reference to the lateral axis is also important. For each item of weight existing to the left of the fuselage centerline, there is an equal weight existing at a corresponding location on the right. This may be upset, however, by unbalanced lateral loading.
The position of the lateral CG is not computed, but the pilot must be aware that adverse effects will certainly arise as a result of a laterally unbalanced condition.
Lateral unbalance will occur if the fuel load is mismanaged by supplying the engine(s) unevenly from tanks on one side of the airplane. The pilot can compensate for the resulting wing-heavy condition by adjusting the aileron trim tab or by holding a constant aileron control pressure. However, this places the airplane controls in an out-of-streamline condition, increases drag, and results in decreased operating efficiency. Since lateral balance is relatively easy to control and longitudinal balance is more critical, further reference to balance on this webpage will mean longitudinal location of the center of gravity.
In any event, flying an airplane that is out of balance can produce increased pilot fatigue with obvious effects on the safety and efficiency of flight. The pilot’s natural correction for longitudinal unbalance is a change of trim to remove the excessive control pressure.
Excessive trim, however, has the effect of not only reducing aerodynamic efficiency but also reducing primary control travel distance in the direction the trim is applied.
Effects of adverse balance
Adverse balance conditions affect airplane flight characteristics in much the same manner as those mentioned for an excess weight condition. In addition, there are two essential airplane characteristics that may be seriously affected by improper balance; these are stability and control. Loading in a nose-heavy condition causes problems in controlling and raising the nose, especially during takeoff and landing. Loading in a tail-heavy condition has a most serious effect upon longitudinal stability, and can reduce the airplane’s capability to recover from stalls and spins. Another undesirable characteristic produced from tail-heavy loading is that it produces very light control forces. This makes it easy for the pilot to inadvertently overstress the airplane.
Limits for the location of the airplane’s center of gravity are established by the manufacturer. These are the fore and aft limits beyond which the CG should not be located for flight. These limits are published for each airplane in the Type Certificate Data Sheet, or Aircraft Specification and the Airplane Flight Manual or Pilot’s Operating Handbook (AFM/POH). If, after loading, the CG is not within the allowable limits, it will be necessary to relocate some items within the airplane before flight is attempted.
The forward center-of-gravity limit is often established at a location that is determined by the landing characteristics of the airplane. During landing, which is one of the most critical phases of flight, exceeding the forward CG limit may result in excessive loads on the nosewheel; a tendency to nose over on tailwheel type airplanes; decreased performance; higher stalling speeds; and higher control forces. In extreme cases, a CG location that is forward of the forward limit may result in nose heaviness to the extent that it may be difficult or impossible to flare for landing.
Manufacturers purposely place the forward CG limit as far rearward as possible to aid pilots in avoiding damage to the airplane when landing. In addition to decreased static and dynamic longitudinal stability, other undesirable effects caused by a CG location aft of the allowable range may include extreme control difficulty, violent stall characteristics, and very light stick forces that make it easy to overstress the airplane inadvertently.
A restricted forward center-of-gravity limit is also specified to assure that sufficient elevator deflection is available at minimum airspeed. When structural limitations or large stick forces do not limit the forward CG position, it is located at the position where full-up elevator is required to obtain a high angle of attack for landing.
The aft center-of-gravity limit is the most rearward position at which the CG can be located for the most critical maneuver or operation. As the CG moves aft, a less stable condition occurs, which decreases the ability of the airplane to right itself after maneuvering or turbulence.
For some airplanes the CG limits, both fore and aft, may be specified to vary as gross weight changes. They may also be changed for certain operations such as acrobatic flight, retraction of the landing gear, or the installation of special loads and devices that change the flight characteristics.
The actual location of the CG can be altered by many variable factors and is usually controlled by the pilot.
Placement of baggage and cargo items determines the CG location. The assignment of seats to passengers can also be used as a means of obtaining a favorable balance. If the airplane is tail-heavy, it is only logical to place heavy passengers in forward seats. Also, fuel burn can affect the CG based on the location of the fuel tanks.
Management of weight and balance control
Weight and balance control should be a matter of concern to all pilots. The pilot has control over loading and fuel management (the two variable factors that can change both total weight and CG location) of a particular airplane.
The airplane owner or operator should make certain that up-to-date information is available in the airplane for the pilot’s use, and should ensure that appropriate entries are made in the airplane records when repairs or modifications have been accomplished. Weight changes must be accounted for and the proper notations made in weight and balance records. The equipment list must be updated, if appropriate. Without such information, the pilot has no foundation upon which to base the necessary calculations and decisions.
Before any flight, the pilot should determine the weight and balance condition of the airplane. Simple and orderly procedures, based on sound principles, have been devised by airplane manufacturers for the determination of loading conditions. The pilot must use these procedures and exercise good judgment. In many modern airplanes, it is not possible to fill all seats, baggage compartments, and fuel tanks, and still remain within the approved weight and balance limits.
If the maximum passenger load is carried, the pilot must often reduce the fuel load or reduce the amount of baggage.
Terms and definitions
The pilot should be familiar with terms used in working the problems related to weight and balance. The following list of terms and their definitions is well standardized, and knowledge of these terms will aid the pilot to better understand weight and balance calculations of any airplane. Terms defined by the General Aviation Manufacturers Association as an industry standard are marked in the titles with GAMA.
• Arm (moment arm)—is the horizontal distance in inches from the reference datum line to the center of gravity of an item. The algebraic sign is plus (+) if measured aft of the datum, and minus (–) if measured forward of the datum.
• Basic empty weight (GAMA)—includes the standard empty weight plus optional and special equipment that has been installed.
• Center of gravity (CG)—is the point about which an airplane would balance if it were possible to suspend it at that point. It is the mass center of the airplane, or the theoretical point at which the entire weight of the airplane is assumed to be concentrated. It may be expressed in inches from the reference datum, or in percent of mean aerodynamic chord (MAC).
• Center-of-gravity limits—are the specified forward and aft points within which the CG must be located during flight. These limits are indicated on pertinent airplane specifications.
• Center-of-gravity range—is the distance between the forward and aft CG limits indicated on pertinent airplane specifications.
• Datum (reference datum)—is an imaginary vertical plane or line from which all measurements of arm are taken. The datum is established by the manufacturer. Once the datum has been selected, all moment arms and the location of CG range are measured from this point.
• Delta—is a Greek letter expressed by the symbol Δ to indicate a change of values. As an example, ΔCG indicates a change (or movement) of the CG.
• Floor load limit—is the maximum weight the floor can sustain per square inch/foot as provided by the manufacturer.
• Fuel load—is the expendable part of the load of the airplane. It includes only usable fuel, not fuel required to fill the lines or that which remains trapped in the tank sumps.
• Licensed empty weight—is the empty weight that consists of the airframe, engine(s), unusable fuel, and undrainable oil plus standard and optional equipment as specified in the equipment list. Some manufacturers used this term prior to GAMA standardization.
• Maximum landing weight—is the greatest weight that an airplane normally is allowed to have at landing.
• Maximum ramp weight—is the total weight of a loaded aircraft, and includes all fuel. It is greater than the takeoff weight due to the fuel that will be burned during the taxi and runup operations.
Ramp weight may also be referred to as taxi weight.
• Maximum takeoff weight—is the maximum allowable weight for takeoff.
• Maximum weight—is the maximum authorized weight of the aircraft and all of its equipment as specified in the Type Certificate Data Sheets (TCDS) for the aircraft.
• Maximum zero fuel weight (GAMA)—is the maximum weight, exclusive of usable fuel.
• Mean aerodynamic chord (MAC)—is the average distance from the leading edge to the trailing edge of the wing.
• Moment—is the product of the weight of an item multiplied by its arm. Moments are expressed in pound-inches (lb-in). Total moment is the weight of the airplane multiplied by the distance between the datum and the CG.
• Moment index (or index)—is a moment divided by a constant such as 100, 1,000, or 10,000. The purpose of using a moment index is to simplify weight and balance computations of airplanes where heavy items and long arms result in large, unmanageable numbers.
• Payload (GAMA)—is the weight of occupants, cargo, and baggage.
• Standard empty weight (GAMA)—consists of the airframe, engines, and all items of operating equipment that have fixed locations and are permanently installed in the airplane; including fixed ballast, hydraulic fluid, unusable fuel, and full engine oil.
• Standard weights—have been established for numerous items involved in weight and balance computations. These weights should not be used if actual weights are available. Some of the standard weights are:
| Gasoline | 6 lb/US gal |
| Jet A, Jet A-1 | 6.8 lb/US gal |
| Jet B | 6.5 lb/US gal |
| Oil | 7.5 lb/US gal |
| Water | 8.35 lb/US gal |
• Station—is a location in the airplane that is identified by a number designating its distance in inches from the datum. The datum is, therefore, identified as station zero. An item located at station +50 would have an arm of 50 inches.
• Useful load—is the weight of the pilot, copilot, passengers, baggage, usable fuel, and drainable oil. It is the basic empty weight subtracted from the maximum allowable gross weight. This term applies to general aviation aircraft only.
Basic principles of weight and balance computations
It might be advantageous at this point to review and discuss some of the basic principles of how weight and balance can be determined. The following method of computation can be applied to any object or vehicle where weight and balance information is essential; but to fulfill the purpose of this page, it is directed primarily toward the airplane.
By determining the weight of the empty airplane and adding the weight of everything loaded on the airplane, a total weight can be determined. This is quite simple; but to distribute this weight in such a manner that the entire mass of the loaded airplane is balanced around a point (CG), which must be located within specified limits, presents a greater problem, particularly if the basic principles of weight and balance are not understood.
The point where the airplane will balance can be determined by locating the center of gravity, which is, as stated in the definitions of terms, the imaginary point where all the weight is concentrated. To provide the necessary balance between longitudinal stability and elevator control, the center of gravity is usually located slightly forward of the center of lift. This loading condition causes a nose-down tendency in flight, which is desirable during flight at a high angle of attack and slow speeds.
A safe zone within which the balance point (CG) must fall is called the CG range. The extremities of the range are called the forward CG limits and aft CG limits.
These limits are usually specified in inches, along the longitudinal axis of the airplane, measured from a datum reference. The datum is an arbitrary point, established by airplane designers, which may vary in location between different airplanes.
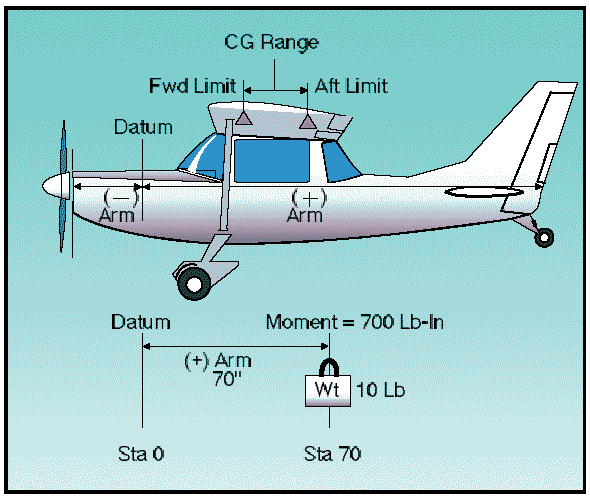
Figure 2: Weight and balance illustrated.
The distance from the datum to any component part of the airplane, or any object loaded on the airplane, is called the arm. When the object or component is located aft of the datum, it is measured in positive inches; if located forward of the datum, it is measured as negative inches, or minus inches. The location of the object or part is often referred to as the station. If the weight of any object or component is multiplied by the distance from the datum (arm), the product is the moment. The moment is the measurement of the gravitational force that causes a tendency of the weight to rotate about a point or axis and is expressed in pound-inches.
To illustrate, assume a weight of 50 pounds is placed on the board at a station or point 100 inches from the datum. The downward force of the weight can be determined by multiplying 50 pounds by 100 inches, which produces a moment of 5,000 lb-in.
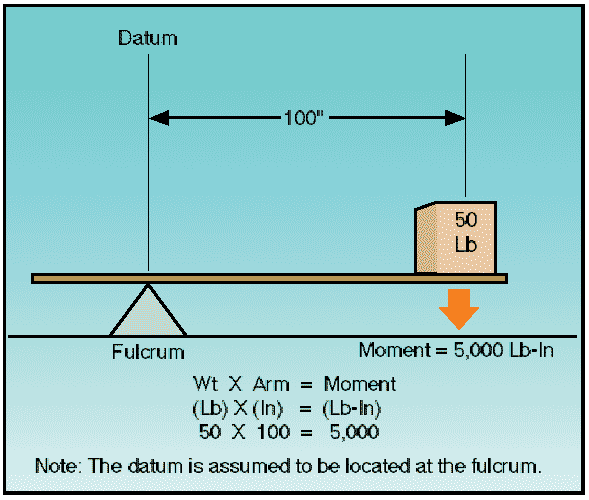
Figure 3: Determining moments.
To establish a balance, a total of 5,000 lb-in must be applied to the other end of the board. Any combination of weight and distance which, when multiplied, produces a 5,000 lb-in moment will balance the board. For example, as illustrated in figure 4, if a 100-pound weight is placed at a point (station) 25 inches from the datum, and another 50-pound weight is placed at a point (station) 50 inches from the datum, the sum of the product of the two weights and their distances will total a moment of 5,000 lb-in, which will balance the board.
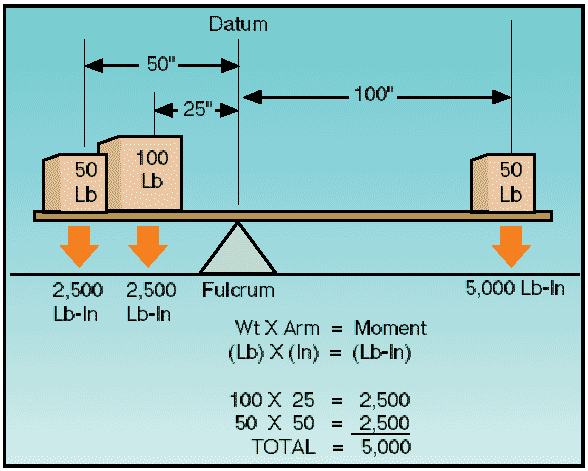
Figure 4: Establishing a balance.
Weight and balance restrictions
The airplane’s weight and balance restrictions should be closely followed. The loading conditions and empty weight of a particular airplane may differ from that found in the AFM/POH because modifications or equipment changes may have been made. Sample loading problems in the AFM/POH are intended for guidance only; therefore, each airplane must be treated separately. Although an airplane is certified for a specified maximum gross takeoff weight, it will not safely take off with this load under all conditions.
Conditions that affect takeoff and climb performance such as high elevations, high temperatures, and high humidity (high-density altitudes) may require a reduction in weight before flight is attempted. Other factors to consider prior to takeoff are runway length, runway surface, runway slope, surface wind, and the presence of obstacles. These factors may require a reduction in weight prior to flight.
Some airplanes are designed so that it is difficult to load them in a manner that will place the CG out of limits. These are usually small airplanes with the seats, fuel, and baggage areas located near the CG limit.
These airplanes, however, can be overloaded in weight.
Other airplanes can be loaded in such a manner that they will be out of CG limits even though the useful load has not been exceeded.
Because of the effects of an out-of-balance or overweight condition, a pilot should always be sure that an airplane is properly loaded.
Determining loaded weight and center of gravity
There are various methods for determining the loaded weight and center of gravity of an aircraft. There is the computation method, as well as methods that utilize graphs and tables provided by the aircraft manufacturer.
Computational method
The computational method involves the application of basic math functions. The following is an example of the computational method.
Given:
| Maximum Gross Weight | 3400 lb |
| Center-of-Gravity Range | 78-86 in |
| Front Seat Occupants | 340 lb |
| Rear Seat Occupants | 350 lb |
| Fuel | 75 gal |
| Baggage Area 1 | 80 lb |
To determine the loaded weight and CG, follow these steps.
Step 1—List the weight of the airplane, occupants, fuel, and baggage. Remember that fuel weighs 6 pounds per gallon.
Step 2—Enter the moment for each item listed. Remember “weight x arm = moment.”
Step 3—Total the weight and moments.
Step 4—To determine the CG, divide the total moment by the total weight.
NOTE: The weight and balance records for a particular airplane will provide the empty weight and moment as well as the information on the arm distance.
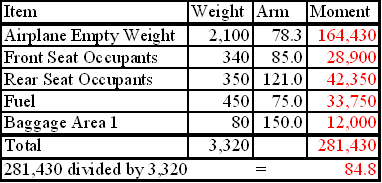
The total loaded weight of 3,320 pounds does not exceed the maximum gross weight of 3,400 pounds and the CG of 84.8 is within the 78-86 inch range; therefore, the airplane is loaded within limits.
Graph method
Another method for determining the loaded weight and CG is the use of graphs provided by the manufacturers.
To simplify calculations, the moment may sometimes be divided by 100, 1,000, or 10,000. The following is an example of the graph method.
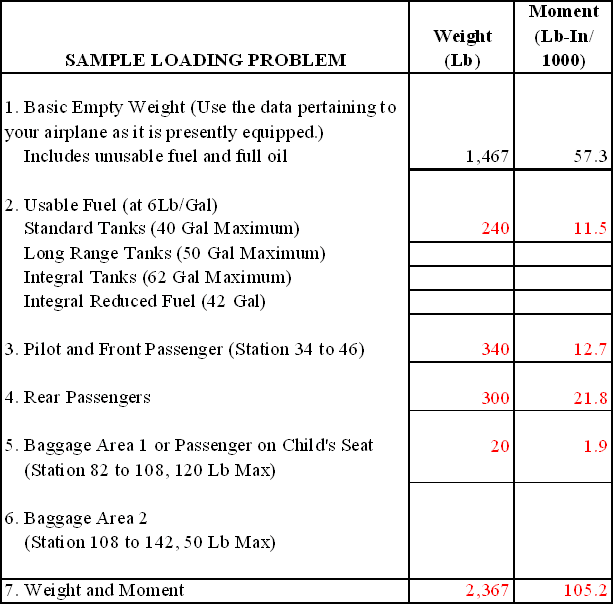
Figure 5: Weight and balance data.
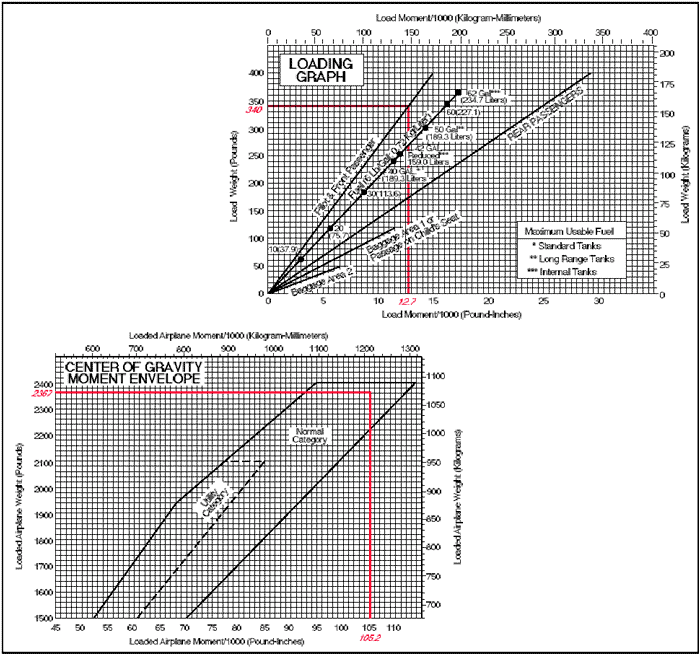
Figure 6: CG moment envelope and loading graph.
Given:
| Front Seat Occupants | 340 lb |
| Rear Seat Occupants | 300 lb |
| Fuel | 40 gal |
| Baggage Area 1 | 20 lb |
The same steps should be followed as in the computational method except the graphs provided will calculate the moments and allow the pilot to determine if the airplane is loaded within limits. To determine the moment using the loading graph, find the weight and draw a line straight across until it intercepts the item for which the moment is to be calculated. Then draw a line straight down to determine the moment. (The red line on the loading graph represents the moment for the pilot and front passenger. All other moments were determined in the same way.) Once this has been done for each item, total the weight and moments and draw a line for both weight and moment on the center-of-gravity envelope graph. If the lines intersect within the envelope, the airplane is loaded within limits. In this sample loading problem, the airplane is loaded within limits.
Table method
The table method applies the same principles as the computational and graph methods. The information and limitations are contained in tables provided by the manufacturer. Figure 7 is an example of a table and a weight and balance calculation based on that table. In this problem, the total weight of 2,799 pounds and moment of 2,278/100 are within the limits of the table.
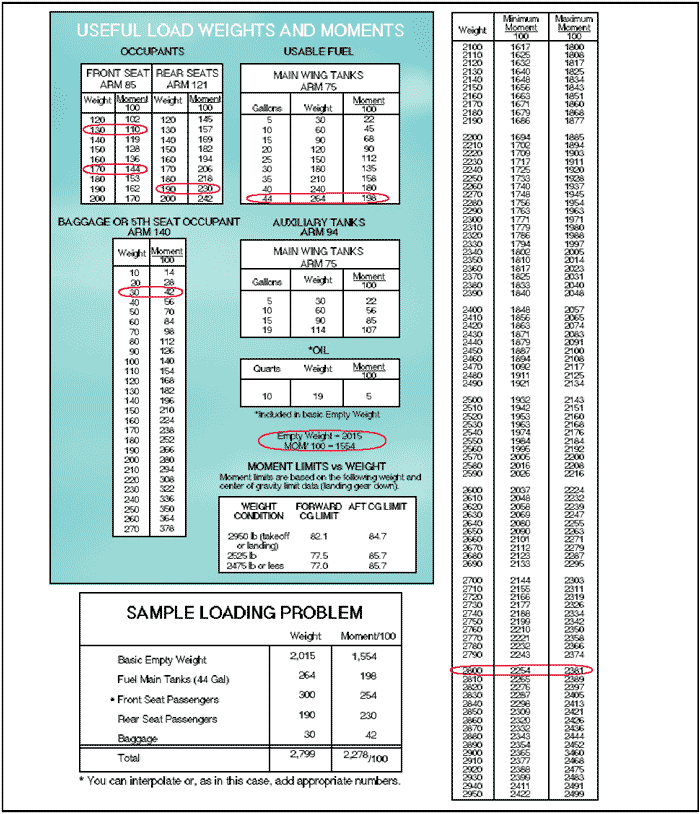
Figure 7: Loading schedule placard.
Computations with a negative arm
Figure 8 is a sample of weight and balance computation using an airplane with a negative arm. It is important to remember that a positive times a negative equals a negative, and a negative would be subtracted from the total moments.
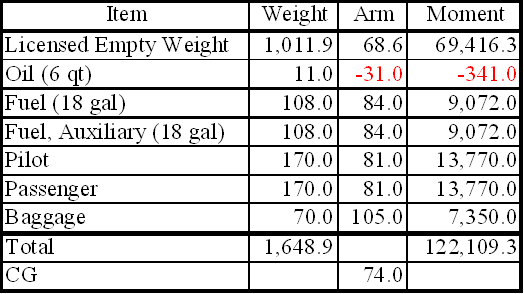
Figure 8: Sample weight and balance using a negative.
Computations with zero fuel weight
Figure 9 is a sample of weight and balance computation using an airplane with a zero fuel weight. In this example, the total weight of the airplane less fuel is 4,240 pounds, which is under the zero fuel weight of 4,400 pounds. If the total weight of the airplane without fuel had exceeded 4,400 pounds, passengers or cargo would have to be reduced to bring the weight at or below the max zero fuel weight.
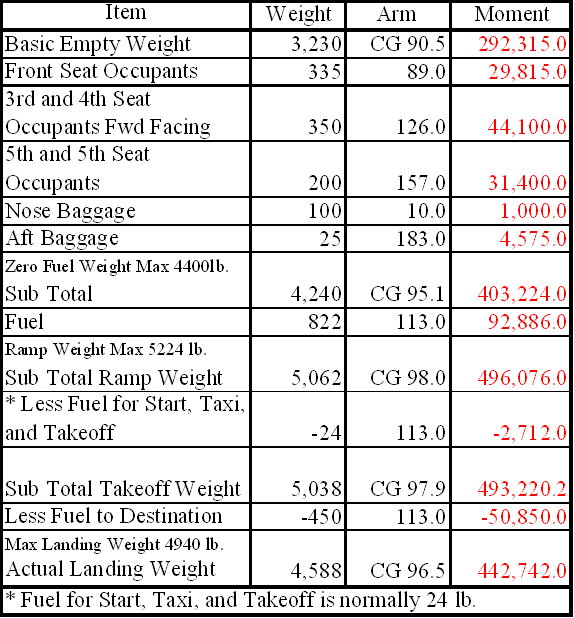
Figure 9: Sample weight and balance using an airplane with a published zero fuel weight.
Shifting, adding, and removing weight
A pilot must be able to accurately and rapidly solve any problems that involve the shift, addition, or removal of weight. For example, the pilot may load the aircraft within the allowable takeoff weight limit, then find a CG limit has been exceeded. The most satisfactory solution to this problem is to shift baggage, passengers, or both. The pilot should be able to determine the minimum load shift needed to make the aircraft safe for flight. Pilots should be able to determine if shifting a load to a new location will correct an out-of-limit condition. There are some standardized calculations that can help make these determinations.
Weight shifting
When weight is shifted from one location to another, the total weight of the aircraft is unchanged. The total moments, however, do change in relation and proportion to the direction and distance the weight is moved.
When weight is moved forward, the total moments decrease; when weight is moved aft, total moments increase. The moment change is proportional to the amount of weight moved. Since many aircraft have forward and aft baggage compartments, weight may be shifted from one to the other to change the CG. If starting with a known aircraft weight, CG, and total moments, calculate the new CG (after the weight shift) by dividing the new total moments by the total aircraft weight.
To determine the new total moments, find out how many moments are gained or lost when the weight is shifted. Assume that 100 pounds has been shifted from station 30 to station 150. This movement increases the total moments of the aircraft by 12,000 lb-in.
| Moment when at station 150 | = | 100 lb x 150 in | = | 15,000 lb-in |
| Moment when at station 30 | = | 100 lb x 30 in | = | 3,000 lb-in |
| Moment change | = | 12,000 lb-in | | |
By adding the moment change to the original moment (or subtracting if the weight has been moved forward instead of aft), the new total moments are obtained.
Then determine the new CG by dividing the new moments by the total weight:
| Total moments | = | 616,000 + 12,000 | = | 628,000 |
| CG | = | 628,000/8,000 (Total weight) | = | 78.5 in |
The shift has caused the CG to shift to station 78.5
A simpler solution may be obtained by using a computer or calculator and a proportional formula. This can be done because the CG will shift a distance that is proportional to the distance the weight is shifted.
EXAMPLE
| Weight Shifted/Total Weight | = | ΔCG (change of CG)/Distance weight is shifted |
| 100/8,000 | = | ΔCG/120 |
| ΔCG | = | 1.5 in |
The change of CG is added to (or subtracted from when appropriate) the original CG to determine the new CG:
| 77 + 1.5 | = | 78.5 inches aft of datum |
The shifting weight proportion formula can also be used to determine how much weight must be shifted to achieve a particular shift of the CG. The following problem illustrates a solution of this type.
EXAMPLE
Given:
| Aircraft Total Weight | 7,800 lb |
| CG | Station 81.5 |
| Aft CG Limit | 80.5 |
Determine how much cargo must be shifted from the aft cargo compartment at station 150 to the forward cargo compartment at station 30 to move the CG to exactly the aft limit.
Solution:
| Weight to be Shifted/Total Weight | = | ΔCG/Distance weight is shifted |
| Weight to be Shifted/7,800 | = | 1.0 in/120 in |
| Weight to be Shifted | = | 65 lb |
Weight addition or removal
In many instances, the weight and balance of the aircraft will be changed by the addition or removal of weight. When this happens, a new CG must be calculated and checked against the limitations to see if the location is acceptable. This type of weight and balance problem is commonly encountered when the aircraft burns fuel in flight, thereby reducing the weight located at the fuel tanks. Most small aircraft are designed with the fuel tanks positioned close to the CG; therefore, the consumption of fuel does not affect the CG to any great extent.
The addition or removal of cargo presents a CG change problem that must be calculated before flight. The problem may always be solved by calculations involving total moments. A typical problem may involve the calculation of a new CG for an aircraft which, when loaded and ready for flight, receives some additional cargo or passengers just before departure time.
EXAMPLE
Given:
| Aircraft Total Weight | 6,860 lb |
| CG Station | 80.0 |
Determine the location of the CG if 140 pounds of baggage is added to station 150.
Solution:
| Added Weight/ New Total Weight | = | ΔCG/ Distance between weight and old CG |
| 140/(6,860 + 140) | = | ΔCG/(150–80) |
| 140/ 7,000 | = | ΔCG/70 |
| CG | = | 1.4 in aft |
Add ΔCG to old CG
| New CG | = | 80.0 in + 1.4 in | = | 81.4 in |
EXAMPLE
Given:
| Aircraft Total Weight | 6,100 lb |
| CG Station | 80.0 |
Determine the location of the CG if 100 pounds is removed from station 150.
Solution:
| Weight Removed/New Total Weight | = | ΔCG/ Distance between weight and old CG |
| 100/(6,100 – 100) | = | ΔCG/(150 – 80) |
| 100/6,000 | = | ΔCG/70 |
| CG | = | 1.2 in forward |
Subtract ΔCG from old CG
| New CG | = | 80 in - 1.2 in | = | 78.8 in |
In the previous examples, the ΔCG is either added or subtracted from the old CG. Deciding which to accomplish is best handled by mentally calculating which way the CG will shift for the particular weight change. If the CG is shifting aft, the ΔCG is added to the old CG; if the CG is shifting forward, the ΔCG is subtracted from the old CG.